要找到圆的半径,已知其一般方程,我们首先需要将一般方程重写为标准方程,圆的一般方程形式为:
\[Ax^2 + Ay^2 + Bx + Cy + D = 0\]
\(A \neq 0\),为了将其转换为标准方程,我们遵循以下步骤:
1、将 \(x\) 和 \(y\) 项分组:
\[Ax^2 + Ay^2 + Bx + Cy + D = 0\]
可以重写为:
\[A(x^2 + \frac{B}{A}x + y^2 + \frac{C}{A}y) + D = 0\]
2、从 \(x\) 和 \(y\) 项中提取 \(A\):
\[A(x^2 + \frac{B}{A}x + y^2 + \frac{C}{A}y) = -D\]
3、对 \(x\) 和 \(y\) 完成平方:
为了对 \(x\) 完成平方,我们取 \(x\) 的系数的一半,即 \(\frac{B}{A}\),除以 2 得到 \(\frac{B}{2A}\),然后平方得到 \(\left(\frac{B}{2A}\right)^2 = \frac{B^2}{4A^2}\),同样,为了对 \(y\) 完成平方,我们取 \(y\) 的系数的一半,即 \(\frac{C}{A}\),除以 2 得到 \(\frac{C}{2A}\),然后平方得到 \(\left(\frac{C}{2A}\right)^2 = \frac{C^2}{4A^2}\),在方程中添加和减去这些平方,我们得到:
\[A\left(x^2 + \frac{B}{A}x + \frac{B^2}{4A^2} - \frac{B^2}{4A^2} + y^2 + \frac{C}{A}y + \frac{C^2}{4A^2} - \frac{C^2}{4A^2}\right) = -D\]
简化括号内的表达式,我们有:
\[A\left(\left(x + \frac{B}{2A}\right)^2 - \frac{B^2}{4A^2} + \left(y + \frac{C}{2A}\right)^2 - \frac{C^2}{4A^2}\right) = -D\]
分配 \(A\),我们得到:
\[A\left(x + \frac{B}{2A}\right)^2 - \frac{AB^2}{4A^2} + A\left(y + \frac{C}{2A}\right)^2 - \frac{AC^2}{4A^2} = -D\]
简化分数,我们有:
\[A\left(x + \frac{B}{2A}\right)^2 - \frac{B^2}{4A} + A\left(y + \frac{C}{2A}\right)^2 - \frac{C^2}{4A} = -D\]
将常数项移到方程的另一侧,我们得到:
\[A\left(x + \frac{B}{2A}\right)^2 + A\left(y + \frac{C}{2A}\right)^2 = \frac{B^2}{4A} + \frac{C^2}{4A} - D\]
在右侧提取 \(\frac{1}{4A}\),我们得到:
\[A\left(x + \frac{B}{2A}\right)^2 + A\left(y + \frac{C}{2A}\right)^2 = \frac{B^2 + C^2 - 4AD}{4A}\]
将两边除以 \(A\),我们得到:
\[\left(x + \frac{B}{2A}\right)^2 + \left(y + \frac{C}{2A}\right)^2 = \frac{B^2 + C^2 - 4AD}{4A^2}\]
4、识别圆的标准方程:
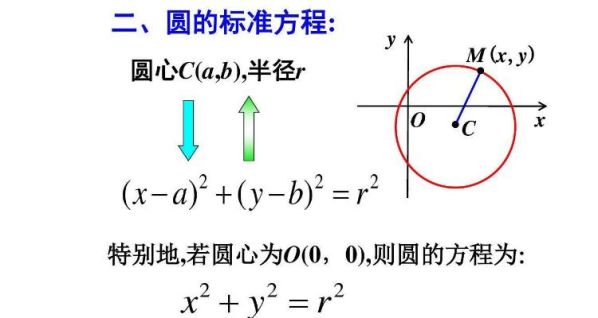
圆的标准方程形式为:
\[(x - h)^2 + (y - k)^2 = r^2\]
\((h, k)\) 是圆心,\(r\) 是半径,从方程 \(\left(x + \frac{B}{2A}\right)^2 + \left(y + \frac{C}{2A}\right)^2 = \frac{B^2 + C^2 - 4AD}{4A^2}\),我们可以看到圆心是 \(\left(-\frac{B}{2A}, -\frac{C}{2A}\right)\),半径 \(r\) 是:
\[r = \sqrt{\frac{B^2 + C^2 - 4AD}{4A^2}} = \frac{\sqrt{B^2 + C^2 - 4AD}}{2A}\]
圆的半径是:
\[\frac{\sqrt{B^2 + C^2 - 4AD}}{2A}\]
本文来自作者[语蓉琳风韵]投稿,不代表臻货网立场,如若转载,请注明出处:https://www.zhenhuowang.com/zhuanlan/202501-968.html


评论列表(3条)
我是臻货网的签约作者“语蓉琳风韵”!
希望本篇文章《圆的标准方程求半径 已知圆的一般方程求半径》能对你有所帮助!
本篇文章概览:要找到圆的半径,已知其一般方程,我们首先需要将一般方程重写为标准方程,圆的一般方程形式为:\[Ax^2 + Ay^2 + Bx + Cy + D = 0\]\(A \neq 0...